4.2 Yaw of Repose and Resulting Crossrange Deflection
Referring to Figure 4.1-1, as the bullet flies, the principal aerodynamic force on the bullet acts directly opposite to the velocity vector. The projection of this force along the longitudinal axis is the drag force on the bullet. The drag force acts through both the center of pressure and the center of mass, and so it does not create a torque on the bullet. With a tiny yaw angle (i.e., the yaw of repose) a very small component of the aerodynamic force acts horizontally and sideward on the bullet. This small sideforce, acting at the
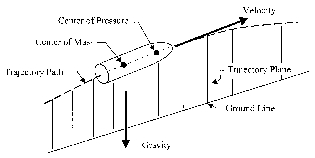
Figure 4.1-1 Bullet Flight Characteristics
center of pressure, creates a torque on the bullet equal to the force multiplied by the moment arm, that is, the distance between the center of mass and the center of pressure. The direction of this torque is downward for a right hand spinning bullet, or upward for a left-hand spinning bullet.
To visualize this situation refer to Figure 4.2-1, which is Figure 4.1-1 viewed from directly above the bullet. Note that there is no wind acting in Figure 4.2-1. The principal trajectory parameters are displayed with the correct relationships for a bullet with a right hand spin. The velocity vector V is in the trajectory plane and tangent to the trajectory path. The aerodynamic force Faero is directed opposite to the velocity vector. The bullet has a spin angular momentum H that is directed along the longitudinal axis and forward for a right-hand spin. The yaw of repose is the small angle between the H vector and the V vector. This angle causes a small component of the aerodynamic force, called Fside, to act on the side of the bullet, and which can be thought of as acting at the center of pressure of the bullet. This sideforce creates a torque vector M on the bullet. The torque vector M is the vector cross product of the moment arm r, which extends from the center of mass to the center of pressure, and the sideforce Fside. The direction of the torque vector M is downward, that is, perpendicular to the plane containing r and Fside. The torque vector does not point exactly vertically downward, because of the inclination angle of the trajectory, but it is exactly perpendicular to the plane of r and Fside.
Now consider the angular motion of the bullet, which is governed by the equations of angular motion. A key parameter in these equations is the angular momentum of the bullet, which consists of two components. The first component is the spin angular momentum H shown in Figure 4.2-1, which is large in order to guarantee stabilization of the bullet. Because the bullet rotates downward in the pitch direction as it flies, a second component of

angular momentum is directed horizontally in the direction opposite to Fside. This component is so small that it can be considered negligible compared to the spin angular momentum.
The magnitude of the spin angular momentum of a bullet is nearly constant as the bullet flies. It changes very slowly because the rotational frictional force and torque acting on the bullet are small. Consequently, the change in the vector angular momentum of the bullet as it flies is very nearly limited to a change in direction of the spin angular momentum vector H, with no change in the magnitude of that quantity. Under this condition, the equations of angular motion tell us that the angular momentum vector H rotates toward the torque vector M applied to the bullet.
Consequently, the spin angular momentum vector H, which is always along the central axis of the bullet, rotates downward toward the torque vector M caused by the sideforce Fside. So, in essence the sideforce causes the bullet to rotate downward in the pitch direction to keep the axis of the bullet almost exactly tangent to the trajectory curve as the bullet flies along the trajectory arc. Of course, as the axis of the bullet and the vector H rotate downward, the vector M also rotates at exactly the same rate, so that H always remains perpendicular to M. This entire situation is almost a steady state motion; everything changes very slowly as the bullet flies. The yaw of repose angle, the spin angular momentum magnitude, the torque magnitude, and the sideforce are nearly, but not quite, constant as the bullet flies from muzzle to target.
Because the sideforce Fside acts throughout the flight of the bullet, a horizontal (crossrange) deflection of the bullet will result. This deflection is generally small, but it can be noticed, especially by long-range target shooters. This is because the deflection increases as time of flight to the target grows longer. Usually the observation comes about as follows. A rifle is sighted in at point of aim, say, at 200 yards. Then the range to the target is changed to 400 yards. The shooter makes an elevation correction to the rifle sights for the longer range, and a sighting shot (or group) is fired. The shooter notices that the shot (or group) is deflected to the right (for a RH twist barrel) by a few inches, but there is no crosswind to account for this deflection. The shooter can apply a windage correction for the 400-yard range, and everything goes well at that range distance. Then, if the range is changed to 600 yards, the shooter has the same experience. A satisfactory sight elevation correction can be made, but shots will be deflected a few inches to the right, necessitating a windage correction even in the absence of a crosswind. The sideforce arising from the yaw of repose is the cause of this unexpected crossrange deflection of bullets. [Here we assume that the crosshairs in the telescope (and the adjustment axes) are aligned precisely vertically and horizontally, so that the sight adjustments are precisely vertical and horizontal.] Crossrange deflections occur also for bullets with left-hand spin, but the deflections are toward the left rather than toward the right. For a bullet with left-hand spin, the spin angular momentum vector is directed out of the tail of the bullet. To cause the bullet to rotate downward in pitch, an upward vertical torque is necessary so that the angular momentum vector will rotate upward. This in turn requires a sideforce directed from right to left across the trajectory plane, and this can result only from a yaw of repose angle to the left of the trajectory plane (a small, nose-left angle of the bullet as it flies). Consequently, the sideforce is directed to the left, and the bullet deflects in the crossrange direction to the left as it flies downrange.
