6.1 Differential Equations of Bullet Motion
In the three-degree-of-freedom analytical model of bullet ballistics, the bullet is considered as a point mass characterized by its mass m and ballistic coefficient C . The bullet moves along a trajectory as shown in Figure 6-1 under the influence of two forces, the aerodynamic drag force Dand the gravitational force mg (where g is the acceleration due to gravity, 32.176 ft/sec 2 in the Northern Hemisphere).
Figure 6-1 also shows the coordinate system used to describe the bullet motion. The origin of the coordinates is at the muzzle of the gun. The x axis is level at the firing point and points downrange. The y axis is vertical at the firing point, so that gravity acts in the negative y direction. The z axis completes a right-handed cartesian coordinate frame, and the x-z plan is horizontal.
The bullet is fired along the extended bore centerline, which is in the x-y plane. In the absence of a crosswind, the bullet trajectory then remains in the x-y plane. In the absence of a crosswind, the bullet trajectory then remains in the x-y plane. The bore line is elevated at an angle X with respect to the x axis. As the bullet flies downrange its trajectory curves downward. At any point on the trajectory (such as the point shown in Figure 6-1 ) the bullet velocity vector V is in the x-y plane and tangent to the trajectory. The aerodynamic drag force D acts directly opposite to V , so it is also in the x-y plane. The velocity vector V is elevated at an angle X relative to a line parallel to the x axis, as shown in the figure. The angle X is positive when the trajectory is rising, as depicted in the figure. After the trajectory peaks and begins to descend, X becomes negative.
The mass of the bullet is its weight divided by the acceleration due to gravity:
(6.1-1)where w is the bullet weight in grains and the factor 7000 converts grains to pounds (7000 grains = 1.0 lb). Equation (6.1-1) expresses the bullet mass in slugs, and mg is bullet weight in pounds.
The differential equations of bullet motion result from applying Newton’s second law to the bullet and resolving the motions and forces along the coordinate axes:
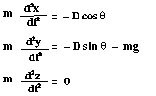(6.1-2) (6.1-3) (6.1-4)In these equations the position coordinates x, y, and z and the angle X are functions of time t . The drag force D also varies with time, but the mass m and the gravitational acceleration g are constants.
The velocity components are defined by
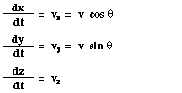(6.1-5)The angle X is the slope angle of the trajectory and is defined by:
(6.1-6)The bullet leaves the muzzle at t = 0, and the initial conditions of the motion are then:
x(0) = y(0) = z(0) = 0
v x (0) = v m cos X
v y (0) = v m sin X (6.1-7)
v z (0) = 0
where v m is the muzzle velocity of the bullet and X is the bore elevation angle defined earlier.
With the initial conditions z(0) = 0 and v z (0) = 0 , equation (6.1-4) has the solution:
for all t . This corresponds, of course, to bullet motion only in the x-y plane. Therefore, the following discussions will be concerned only with the x and y components of the bullet motion.