3.0 Exterior Ballistic Effects on Bullet Flight
When a bullet flies through the air, two types of forces act on the bullet to determine its path (trajectory) through the air. The first is gravitational force; the other is aerodynamics. Several kinds of aerodynamic forces act on a bullet: drag, lift, side forces, Magnus force, spin damping force, pitch damping force, and Magnus cross force. The most important of these aerodynamic forces is drag. All the others are very small in comparison when the bullet is spin-stabilized. To a very good approximation, the drag force and the gravitational force together determine the trajectory of any spin-stabilized bullet. The other small aerodynamic forces cause only small variations from the trajectory that is determined by drag and gravity acting alone on the bullet. For trajectory computation purposes, this allows the bullet to be modeled as a point mass with a ballistic coefficient. In other words, the bullet motion is modeled as a three degrees of freedom (3 DOF) physics problem, that is, as a point mass with three translational degrees of freedom. The bullet trajectory calculated with this approach is almost exactly correct. If we wished to treat the small variations caused by the other aerodynamic forces, it would be necessary to model the bullet as a spinning body with six degrees of freedom (6 DOF), three translational and three rotational degrees of freedom. This approach, while more exact, is very complex in both a physics and a mathematical sense, and it is neither practical nor necessary to use this approach for sporting purposes. In Section 4.0 we will discuss a few 6 DOF effects that can be observed on long range sporting bullet trajectories. However, it will be obvious that we can treat these effects only qualitatively. The only quantitative observation we will be able to make is that these effects are small.
The 3 DOF model of bullet flight is used in all exterior ballistics programs available to handloaders, including Infinity. In the 3 DOF model, the gravitational force always acts vertically downward at the location of the bullet, regardless of the bullet’s orientation relative to the vertical direction.
Aerodynamic drag always acts opposite to the bullet’s direction of travel through the air. That is, drag always tends to slow the bullet down. As the direction of bullet travel changes during the trajectory, so does the direction of the drag force. Drag is a very complex function of bullet velocity relative to the air, and it depends critically on the density of the air and on the speed of sound in the air through which the bullet is moving. Air density, in turn, depends on true barometric pressure, temperature of the air, and relative humidity at the location of the bullet as it flies. These atmospheric parameters depend critically on the altitude of the bullet above sea level. The speed of sound in the air depends primarily on temperature of the air, and so it also depends on altitude at the bullet location.
In addition to gravity and drag, there are other strong effects on the path of a flying bullet. Wind, which is any motion of the air mass through which the bullet is flying, is one such effect. A headwind or tailwind will cause the bullet to experience more or less drag, respectively, than it would if it traveled in still air. A crosswind causes the bullet to turn in the direction that the crosswind is blowing. A vertical wind causes the bullet to turn upward or downward, following the vertical wind that blows upward or downward, respectively. And so, the path of the bullet (trajectory) is changed by winds compared to the path it would have in still air. The 3 DOF model of bullet flight permits the wind effects to be computed almost exactly for a spin-stabilized bullet in an exterior ballistics program such as Infinity.
Shooting uphill or downhill also causes significant changes to the trajectory of a flying bullet compared with its trajectory on a level firing range. In fact, if a gun is sighted in on a level range, a bullet fired either uphill or downhill always shoots high relative to the shooter’s line of sight through the gun sights. Two effects contribute to the trajectory changes. One is geometrical, and we will describe this effect in a later subsection. The other is the fact that when a bullet travels upward or downward relative to the firing point, the density of the air changes, affecting the drag. These trajectory changes also are computed in Sierra’s Infinity program.
The temperature of the propellant (powder) in a cartridge at the instant of ignition can have a strong effect on chamber pressure. If a gun is sighted in on a target range at some temperature, and then is fired in another environment in which the propellant temperature is different, the muzzle velocity of a bullet can be significantly different compared to what it was when the gun was sighted in. The difference in muzzle velocity, of course causes a change in bullet trajectory. The temperature sensitivity of different powders varies from one type to another. Only the manufacturer of any type of powder can quantify the temperature sensitivity of that powder to a handloader. But, an exterior ballistics program can be used to explore the sensitivity of the trajectory of any bullet to changes in muzzle velocity. Sierra’s Infinity program is designed to make this computation especially easy.
All the effects mentioned above are described in more detail in the following subsections of this Section 3.0. They are treated one at a time, so that the reader can determine which are most important for his or her particular shooting application. However, one of the most significant advantages of an exterior ballistics software program like Infinity is that any combination of these effects can be explored for any one or more cartridges. For example, the effect of a wind and altitude change can be computed, or the effect of a change in atmospheric conditions can be determined. Likewise, the effect of a change in muzzle velocity when shooting uphill or downhill can be determined, or a 44 Magnum handgun can be compared with a 44 Magnum rifle. Any other imaginable combination of cartridges and shooting conditions can be explored.
Four more interesting topics are described later in this section. The first is sighting in, or zeroing, a gun at a selected range distance under various shooting conditions. This is a familiar process to almost all shooters, but a number of interesting questions frequently arise. The second topic is Point Blank Range (PBR), which is a very interesting concept for hunters and shooters participating in the silhouette games. PBR is the range distance out to which a shooter can hold his sights directly on a target, without holding over or under, and be assured of a hit. A technique is described to maximize the PBR of any gun/cartridge combination for a target of a given vertical size. A third topic which is of frequent interest to shooters is the maximum range to which a gun/cartridge combination will shoot and the elevation angle of the bore that must be used to achieve that maximum range. Designers of public shooting ranges often address this question. The final topic is the maximum altitude a bullet will reach if a gun is pointed straight up and fired. This is often a question for safety reasons.
As a reference for discussions in the following subsections, we must describe the important parameters of a bullet trajectory. Figure 3.0-1 has been prepared as an aid to this description. A bullet exits the muzzle of a gun in the direction of the extended bore line. After it exits the muzzle, gravity causes the bullet to begin to fall away from the extended bore line. The bullet trajectory then arcs downward, as shown by the bold line in Figure 3.0-1. “Drop” is a term used to denote the vertical distance from a point on the extended bore line to a corresponding point on the trajectory, at any range distance from the muzzle. It is very important to understand that “drop” is measured in the vertical direction (direction of gravity), regardless of whether the barrel of the gun is level (as shown in Figure 3.0-1) or tilted upward or downward. In Figure 3.0-1 the drop (do) at range (Ro) is illustrated.
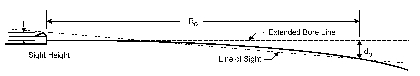
Figure 3.0-1. Illustrating the Parameters of a Bullet Trajectory
The shooter, however, aims the weapon at a target using the line of sight through the gun sights. The line of sight is not parallel to the extended bore line; there is a small angle between the two lines, which is greatly exaggerated in Figure 3.0-1. From the shooter’s point of view through the gun sights, the trajectory begins below the line of sight by a distance equal to the sight height, then rises to cross the line of sight, and then arcs over to again cross the line of sight at a second point called the zero range Ro. The sight height is a very important parameter. With iron sights, it is the distance from the cen-terline of the bore to the tip of the front sight, as shown in the figure. With telescope sights, the sight height can be taken as the distance from the center-line of the bore to the axis of the telescope, which also is the centerline of the objective lens.
“Bullet path” is a term used to denote the perpendicular distance between a point on the line of sight and the corresponding point on the bullet trajectory at any range distance from the muzzle. It is very important to understand that “bullet path” is measured perpendicular to the line of sight regardless of whether the barrel of the gun is level or tilted upward or downward. Bullet path is then a measure of where the bullet would be as “seen” by the shooter, if that were possible. At the muzzle, the bullet path is negative by an amount equal to the sight height, because the bullet starts out below the line of sight. The bullet then rises to first cross the line of sight, and then the bullet path is positive, reaching a maximum value at a distance of about 55% of the zero range distance Ro. The bullet path then decreases to a zero value at the zero range and goes negative at ranges greater than the zero range.
